Given Solar Eclipse Occurs Again years After at the Same Location

Periodicity of Solar Eclipses

Fred Espenak, NASA's GSFC

Index
one.one Eclipse Seasons
1.2 Interval Between Two Successive Solar Eclipses
i.3 Solar Eclipse Repetition
1.four Saros
one.5 Gamma and Saros Serial
1.6 Saros Series Statistics
1.seven Saros and Other Periods
i.8 Saros and Inex
1.9 Saros-Inex Panorama
1.10 Secular Variations in the Saros and Inex
Acknowledgments
References

---

1.1 Eclipse Seasons

The orbit of the Moon around Earth is inclined about 5.ane° to World's orbit effectually the Sun. Equally a event, the Moon's orbit crosses the ecliptic at 2 points or nodes. If New Moon takes place within about 17° of a node[1], then a solar eclipse will be visible from some location on Globe.

The Dominicus makes 1 consummate excursion of the ecliptic in 365.24 days, and so its average athwart velocity is 0.99° per day. At this charge per unit, it takes 34.v days for the Sun to cross the 34° wide eclipse zone centered on each node. Because the Moon's orbit with respect to the Sun has a hateful elapsing of 29.53 days, there will ever be 1 and possibly ii solar eclipses during each 34.five-day interval when the Lord's day passes through the nodal eclipse zones. These time periods are chosen eclipse seasons.

The mid-point of each eclipse flavour is separated by 173.3 days which is the hateful fourth dimension for the Sun to travel from 1 node to the next. The catamenia is a piffling less that half a calendar year because the lunar nodes slowly backslide westward by 19.three° per year.

[1] The actual value ranges from 15.39° to 18.59° considering of the eccentricity of the Moon's (and Globe's) orbit.

---

1.2 Interval Between Two Successive Solar Eclipses

The time interval betwixt any two successive solar eclipses can exist either 1, five, or six lunations (synodic months).

Earth will feel 11,898 eclipses of the Sunday during the 5000-year menstruation from -1999 to +3000 (2000 BCE to 3000 CE [two]). Every bit published in in both the Five Millennium Canon of Solar Eclipses and 5 Millennium Catalog of Solar Eclipses, the distribution of the 11,897 intervals between these eclipses is constitute in Table 1.

Table 1 - Interval Betwixt Successive Solar Eclipses
Number of Lunations	Number of Eclipses	Percent
1	1,361	eleven.4%
5	two,743	23.1%
6	seven,793	65.five%

[ii] The terms BCE and CE are abbreviations for "Before Common Era" and "Common Era," respectively. They are the secular equivalents to the BC and AD dating conventions. (See: Year Dating Conventions )

---

1.iii Solar Eclipse Repetition

Eclipses separated by one, 5 or half-dozen lunations are normally quite dissimilar. They are oftentimes of different types (i.e., partial, annular, total or hybrid) with various Sunday-Moon-World alignment geometries, and with different lunar orbital characteristics (i.e., longitude of perigee and longitude of ascending node). More importantly, these short periods are of no value as predictors of hereafter eclipses because they do not repeat in any recognizable design.

A simple eclipse repetition cycle tin be establish past requiring that certain orbital parameters be repeated. The Moon must be in the new phase with the same longitude of perigee and same longitude of the ascending node. These weather condition are met by searching for an integral multiple in the Moon'south three major periods-the synodic, anomalistic and draconic months. A 4th condition might require that an eclipse occur at approximately the same time of yr to preserve the centric tilt of Earth and thus, the same season, as well equally the altitude from the Dominicus.

---

1.4 Saros

The Saros arises from a harmonic betwixt three of the Moon's orbital cycles. All three periods are field of study to slow variations over long fourth dimension scales, but their electric current values (2000 CE) are:

          Synodic Month (New Moon to New Moon)    = 29.530589 days   = 29d 12h 44m 03s        Anomalistic Calendar month (perigee to perigee)  = 27.554550 days   = 27d 13h 18m 33s        Draconic Month (node to node)           = 27.212221 days   = 27d 05h 05m 36s        

One Saros is equal to 223 synodic months, yet, 239 anomalistic months and 242 draconic months are also equal (within a few hours) to this same menstruation:

          223 Synodic Months        = 6585.3223 days   = 6585d 07h 43m               239 Anomalistic Months    = 6585.5375 days   = 6585d 12h 54m               242 Draconic Months       = 6585.3575 days   = 6585d 08h 35m        

With a period of approximately 6,585.32 days (~eighteen years xi days viii hours), the Saros is valuable tool in investigating the periodicity and recurrence of eclipses. It was first known to the Chaldeans as an interval when lunar eclipses repeat, but the Saros is applicable to solar eclipses as well.

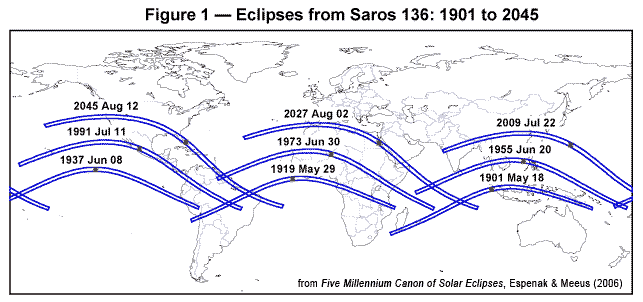
Figure one Eclipses from Saros 136: 1901 to 2045
(click for larger figure)

Any two eclipses separated by one Saros cycle share like characteristics. They occur at the aforementioned node with the Moon at nearly the same distance from Earth and at the aforementioned time of year. Because the Saros period is non equal to a whole number of days, its biggest drawback as an eclipse predictor is that subsequent eclipses are visible from dissimilar parts of the globe. The extra 1/3 day displacement ways that Earth must rotate an additional ~8 hours or ~120° with each wheel. For solar eclipses, this results in a shift of each succeeding eclipse path by ~120° west. Thus, a Saros series returns to approximately the aforementioned geographic region every iii Saros periods (~54 years and 34 days). This triple Saros bicycle is known as the Exeligmos. Figure 1 shows the path of totality for ix eclipses belonging to Saros 136. This serial is of particular involvement because it is currently producing the longest total eclipses of the 20th and 21st centuries. The westward migration of each eclipse path from 1901 through 2045 illustrates the consequences of the extra one/3 day in the Saros menses. The north shift of each path is due to the progressive increase in gamma from -0.3626 (in 1901) to 0.2116 (in 2045). The color figure Recent Eclipses of Saros 136 shows nine eclipse paths from the serial (1937 through 2081).

Saros series do not final indefinitely considering the synodic, draconic, and anomalistic months are not perfectly commensurate with one another. In detail, the Moon's node shifts eastward by well-nigh 0.48° with each eclipse in a series. The post-obit narrative describes the life cycle of a typical Saros series at the Moon'south descending node. The serial begins when the New Moon occurs ~17° east of the node. The Moon'due south umbral/antumbral shadow passes nigh 3500 km south of Globe and a minor fractional eclipse will exist visible from high southern latitudes. One Saros period later, the umbra/antumbra passes ~250 km closer to Globe'southward geocenter (gamma increases) and a partial eclipse of slightly larger magnitude volition result. After almost 10 Saros cycles (~200 years), the first umbral/antumbral eclipse occurs nearly the South Pole of World. Over the course of the next 7 to ten centuries, a key eclipse occurs every 18.031 years (= Saros), just will exist displaced due north by about 250 km with respect to Earth'south centre. Halfway through this period, eclipses of long elapsing occur near the equator (mid-series eclipses may be of brusque duration if hybrid or most so). The last central eclipse of the serial takes place at loftier northern latitudes. Approximately 10 more eclipses will be partial with successively smaller magnitudes. Finally, the Saros series ends 12 to 15 centuries afterwards it began at the opposite pole.

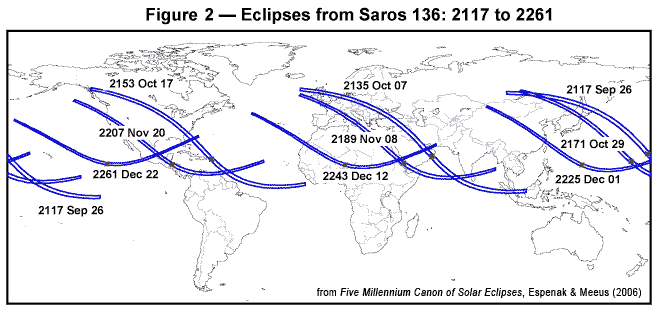
Figure 2 Eclipses from Saros 136: 2117 to 2261
(click for larger figure)

Based on the above description, the path of each umbral/antumbral eclipse should shift uniformly north in latitude after every Saros period. As Fig. 2 shows, this is not always the instance. Ix members from Saros 136 are plotted for the years 2117 through 2261. Although the paths of previous eclipses in this serial were shifting progressively northward (Figure 1), the trend hither is reversed and the paths shift south. This temporary effect is due to the tilt of Earth's axis combined with the passage of Saros 136 eclipses from the Northern Hemisphere'south autumnal equinox through winter solstice. Note that the season for this group of eclipses runs from September through Dec. With each successive eclipse, Globe's Northern Hemisphere tips further and further away from the Lord's day. This motion shifts geographic features and circles of latitude north with respect to the Sunday-Earth line at a rate that is faster than the change in gamma. Consequently, the eclipse paths appear to shift s in latitude until the winter solstice when they again resume a northward tendency.

The scenario for a Saros series at the ascending node is similar except that gamma decreases equally each successive eclipse shifts south of the previous one. The southern breadth trend in eclipse paths reverses to the n near the Northern Hemisphere summer solstice.

Because of the ellipticity of the orbits of Globe and the Moon, the verbal duration and number of eclipses in a complete Saros series is not constant. A series may last 1,226 to 1,551 years and is composed of 69 to 87 eclipses, of which 39 to 59 are umbral/antumbral (i.e., annular, total, or hybrid). At present (2008), in that location are 39 active Saros series numbered 117 to 155. The number of eclipses in each of these series ranges from 70 to 82, however, the bulk of the series (84.half-dozen%) are composed of seventy to 73 eclipses.

Historically speaking, the discussion Saros derives from the Babylonian term "sar" which is an interval of 3600 years. It was never used as an eclipse period until English language astronomer Edmund Halley adopted it in 1691. According to R. H. van Gent, Halley "...extracted it from the dictionary of the 11th-century Byzantine scholar Suidas who in turn erroneously linked information technology to an (unnamed) 223-month Babylonian eclipse menses mentioned by Pliny the Elder (Naturalis Historia 2.10[56])."

---

1.5 Gamma and Saros Series

Gamma changes monotonically throughout any unmarried Saros series. The change in gamma is larger when Earth is well-nigh its aphelion (June to July) than when it is near perihelion (Dec to Jan). For odd numbered series (ascending node), gamma decreases, while for even numbered series (descending node), gamma increases. This simple dominion describes the current beliefs of gamma, but this has not always been the case. The eccentricity of World'southward orbit is presently 0.0167, and is slowly decreasing. It was 0.0181 in the year -2000 and will be 0.0163 in +3000. In the past when the eccentricity was larger, at that place were Saros series in which the trend in gamma reversed for a few cycles before resuming its original direction. These instances occur most perihelion when the Lord's day's apparent motion is highest and may, in fact, overtake the eastward shift of the node. The resulting upshot is a relative shift westward of the node afterwards ane Saros cycle instead of the usual eastward shift. Consequently, gamma reverses management.

The about unusual example of this occurs in Saros series 0. It began in -2955 with 11 partial eclipses, followed by 1 full, 1 hybrid, and 4 annulars. Gamma increased with each eclipse until information technology reversed direction with the 2nd annular. It continued to decrease and the series began to one time over again produce fractional eclipses. With the tertiary partial eclipse, gamma resumed its original due north shift. The series went on to produce 45 more than annular eclipses before ending in the twelvemonth -1675 after 7 partial eclipses.

Among several hundred Saros series examined (-34 to 247), there are many other examples of temporary shifts in the monotonic nature of gamma, although none every bit bizarre as Saros 0. Some serial accept 2 split reversals in gamma (e.one thousand., serial 15, 34, and 52) or fifty-fifty iii (e.grand., series -v and 13). The most recent eclipse with a gamma reversal was in 1674 (Saros 107). The adjacent and final in the Five Millennium Canon and Five Millennium Catalog will occur in 2290 (Saros 165). In past millennia, the gamma reversals were more frequent considering Earth'due south orbital eccentricity was larger.

---

1.half-dozen Saros Series Statistics

Eclipses belonging to 204 different Saros serial fall within the five millennium span of the Canon and Itemize . Two series (-13 and 190) accept only one or ii members represented, while 81 accept a larger but incomplete subset of their members included (-12 to -26, thirty, 145, 147, and 151 to 189). Finally, 121 consummate Saros series are contained within the Canon and Catalog (27 to 29, 31 to 144, 146, and 148 to 150).

The number of eclipses in each of these series ranges from 69 to 87; even so, over a quarter (27.9%) of the series contain 72 eclipses while nearly three quarters (72.one%) of them have 70 to 73 eclipses. Tabular array ii presents the statistical distribution of the number of eclipses in each Saros series. The judge duration (years) equally a role of the number of eclipses is listed along with the offset five Saros series containing the corresponding number of eclipses.

Table 2 - Number of Solar Eclipses in Saros Serial
Number of Solar Eclipses	Duration (years)	Saros Serial Numbers	Saros Series
69	1226	4	156, 171, 174, 177
seventy	1244	25	104, 116, 122, 123, 131,...
71	1262	40	22, 25, 61, 62, 64,...
72	1280	57	-11, 0, i, 3, 4,...
73	1298	25	-13, -12, -three, ii, five,...
74	1316	10	-8, -1, 9, 17, 31,...
75	1334	8	-ten, -nine, -two, 15, 74,...
76	1352	three	11, 108, 146
77	1370	3	145, 166, 184
78	1388	1	69
79	1406	2	111, 182
fourscore	1424	4	-4, 129, 147, 164
81	1442	ane	109
82	1460	two	71, 127
83	1478	iv	30, 72, 88, 90
84	1496	5	32, 33, 35, 53, seventy
85	1514	4	13, xiv, 16, 51
86	1533	v	-7, -v, 12, 34, 52
87	1551	ane	-6

All Saros serial brainstorm and end with a number of partial eclipses. Amongst the 204 Saros series with members falling within the telescopic of the Catechism and Catalog, the number of partial eclipses in the initial phase ranges from half-dozen to 25. Similarly, the number of partial eclipses in the last phase varies from vi to 24. The middle life of a Saros series is composed of umbral/antumbral eclipses (i.east., annular, total, or hybrid), which range in number from 39 to 59. Table 3 presents the statistical distribution in the number of umbral/antumbral eclipses in the Saros series represented in the Canon and Catalog .

Saros 0 is an exception to the above scheme. After beginning with 11 partial eclipses, Saros 0 proceeds with a total, a hybrid, and an annular eclipse. The series and so reverts back to three more than partial eclipses. It finally resumes with a cord of 45 annular eclipses before catastrophe with seven partial eclipses. This odd behavior is due to the higher orbital eccentricity of Earth in the past and fortuitous timing.

Table 3 - Number of A/T/H Solar Eclipses in Saros Series
Number of A/T/H Eclipses	Elapsing (years)	Number of Series	Saros Series Numbers
39	703	4	110, 144, 162, 165
40	721	nineteen	-6, 31, 34, 37,...
41	739	21	-nine, -3, 12, 13,...
42	757	17	10, 15, 16, 28,...
43	775	30	-viii, -7, -5, -4,...
44	793	18	-ii, 11, 17, 18,...
45	811	7	-12, 29, 48, 77,...
46	829	3	-x, 114, 151
47	847	1	140
48	865	6	-one, 38, 66, 171, 188
49	883	ii	27, 153
l	902	one	103
51	920	ane	0 [three], 190
52	938	four	57, 64, 156, 189
53	956	eight	xl, 101, 116, 133,...
54	974	6	47, 98, 119, 134,...
55	992	14	43, 59, 82, 83,...
56	1010	17	-eleven, 1, 6, 8,...
57	1028	13	3, 4, vii, 20,...
58	1046	10	-13, 2, 21, 26,...
59	1064	2	five, 23

[3] The duration of the A/T/H eclipse sequence of Saros 0 is 974 years considering information technology contains 3 partial eclipses.

A concise summary of all 204 Saros series (-13 to 190) is presented in:

Table 4: Summary of Solar Eclipses in Saros Series -thirteen to 190

The number of eclipses in each series is listed followed past the calendar dates of the first and last eclipses in the Saros. Finally, the chronological sequence of eclipse types in the series is tabulated. The number and type of eclipses varies from one Saros series to the adjacent equally reflected in the sequence multifariousness. Note that the tables make no distinction between central and non-central umbral/antumbral eclipses. The following abbreviations are used in the eclipse sequences:

          P = Partial Eclipse                                 A = Annular Eclipse                                 T = Full Eclipse                                 H = Hybrid Eclipse        

The Catalog of Solar Eclipse Saros Series contains links to 181 web pages, each one listing the details of all eclipses in a particular Saros series:

Itemize of Solar Eclipse Saros Serial

---

1.7 Saros and Other Periods

The numbering system used for the Saros series was introduced past van den Bergh in his book Periodicity and Variation of Solar (and Lunar) Eclipses (1955). He assigned the number i to a pair of solar and lunar eclipse series that were in progress during the 2d millennium BCE based on an extrapolation from von Oppolzer's Catechism der Finsternisse (1887).

There is an interval of 1, 5, or 6 synodic months between any sequential pair of solar eclipses. Interestingly, the number of lunations between ii eclipses permits the conclusion of the Saros series number of the 2nd eclipse when the Saros series number of the commencement eclipse is known. Permit the Saros serial number of the first eclipse in a pair be "southward". The Saros series number of the 2d eclipse can be found from the relationships in Table 5 (Meeus, Grosjean, and Vanderleen, 1966).

Table v - Some Eclipse Periods and Their Relationships to the Saros Number
Number of Synodic Months	Length of Fourth dimension	Saros Series Number	Period Name
1	~i month	due south + 38	Lunation
5	~5 months	south - 33	Short Semester
6	~half-dozen months	s + five	Semester
135	~xi years - 1 month	s + i	Tritos
223	~18 years + 11 days	s	Saros
235	~19 years	s + 10	Metonic Cycle
358	~29 years - 20 days	due south + 1	Inex
669	~54 years + 33 days	s	Exeligmos (Triple Saros)

For more than information on these periods and others, see R. H. van Gent's extensive Catalogue of Eclipse Cycles, and Felix Verbelen's Saros, Inex and Eclipse Cycles.

---

i.eight Saros and Inex

A number of different eclipse cycles were investigated by van den Bergh, merely the most useful were the Saros and the Inex. The Inex is equal to 358 synodic months (~29 years less 20 days), which is very near 388.5 draconic months.

          358   Synodic Months      = x,571.9509 days     = ten,571d 22h 49m           388.5 Draconic Months     = x,571.9479 days     = 10,571d 22h 55m        

The actress 0.5 in the number of draconic months means that eclipses separated by one Inex menstruation occur at opposite nodes. Consequently, an eclipse visible from the Northern Hemisphere will be followed one Inex later by an eclipse visible from the Southern Hemisphere, and vice versa. The Inex is equal to ~383.67 anomalistic months, which is far from an integer number. Thus, eclipses separated past ane Inex will very likely exist of dissimilar types, especially if they are cardinal (i.e., total or annular).

The mean time difference between 358 synodic months and 388.five draconic months making up an Inex is simply 6 min. In comparison, the mean difference between these two cycles in the Saros is 52 min. This ways that after one Inex, the shift of the Moon with respect to the node (+0.04°) is much smaller than for the Saros (-0.48°). While a Saros series lasts 12 to 15 centuries, an Inex series typically lasts 225 centuries and contains about 780 eclipses.

---

i.9 Saros-Inex Panorama

Van den Bergh placed all 8,000 solar eclipses in von Oppolzer's Catechism der Finsternisse (1887) into a large two-dimensional matrix. Each Saros series was arranged as a separate column containing every eclipse in chronological guild. The private Saros columns were then staggered so that the horizontal rows each corresponded to unlike Inex serial. This "Saros-Inex Panorama" proved useful in organizing eclipses. For instance, one step down in the panorama is a modify of one Saros period (6585.32 days) later, while one step to the right is a change of one Inex menses (10571.95 days) subsequently. The rows and columns were then numbered with the Saros and Inex numbers.

Saros-Inex Panorama of Solar Eclipses
(click for larger figure)

The panorama also made information technology possible to predict the approximate circumstances of solar (and lunar) eclipses occurring before or later on the catamenia spanned by von Oppolzer's Canon. The time interval "t" betwixt whatever ii solar eclipses can be found through an integer combination of Saros and Inex periods via the post-obit relationship:

          t = a * i  +  b * southward                              (i)       where             t = interval in days,           i = Inex menstruation of 10571.95 days (358 synodic months),           due south = Saros period of 6585.32 days (223 synodic months), and        a, b = integers (negative, zero, or positive).        

From this equation, a number of useful combinations of Inex and Saros periods tin be employed to extend von Oppolzer's Canon from -1207 back to -1600 using nothing more than than uncomplicated arithmetic (van den Bergh, 1954). The ultimate goal of the try was to a produce an eclipse canon for dating historical events prior to -1207. Periods formed by diverse combinations of Inex and Saros were evaluated in order to satisfy ane or more of the post-obit conditions:

1. The divergence from a multiple of 0.5 draconic months should be small
   (i.e., Moon should be about the same distance from the node).
2. The departure from an integral multiple of anomalistic months should be pocket-sized
   (i.due east., Moon should be nearly the aforementioned altitude from Globe).
3. The deviation from an integral multiple of anomalistic years should be small
   (i.e., eclipse should occur on about the aforementioned agenda date).

No single Inex-Saros combination meets all three criteria, simply in that location are periods that practise a reasonably good task for any one of them. Notation that secular changes in the Moon's elements crusade a particular catamenia to be of high accuracy for a express number of centuries. The straight awarding of the Saros-Inex panorama allows for the determination of eclipse dates in the past (or future); however, the application of the longer Saros-Inex combinations permit the rapid interpretation of a number of eclipse characteristics without lengthy calculations. Tabular array 6 lists several of the most useful periods.

Table 6 - Some Useful Eclipse Periods
Period Name	Catamenia (Inex + Saros)	Period (years)	Use
Heliotrope	58i + 6s	1,787	Geographic longitude of central line
Accuratissima	58i + 9s	1,841	Geographic latitude of primal line
Horologia	110i + 7s	iii,310	Fourth dimension of ecliptic conjunction

Modern digital computers using high precision solar and lunar ephemerides tin can directly predict the dates and circumstances of eclipses. Nevertheless, the Saros and Inex cycles remain useful tools in understanding the periodicity and frequency of eclipses.

An enormous Saros-Inex panorama has been produced past Luca Quaglia and John Tilley in the form of a Microsoft Excel file. It shows 61,775 solar eclipses over a 26,000-yr period from -11,000 to +15,000 organized by Saros and Inex Series.

---

i.10 Secular Variations in the Saros and Inex

Because of long secular variations in the average ellipticity of the Moon's and Earth's orbits, the hateful lengths of the synodic, draconic, and anomalistic months are slowly changing. The hateful synodic and draconic months are increasing by approximately 0.2 and 0.4 s per millennium, respectively. Meanwhile, the anomalistic month is decreasing past about 0.viii due south per millennium.

Although small, the cumulative furnishings of such changes has an impact on both the Saros and Inex. Tabular array vii shows how the number of draconic and anomalistic months change with respect to 223 synodic months (Saros period) over an interval of 7000 years. Of particular involvement is the terminal column, which shows the mean shift of the Moon's node later on a period of one Saros. It is gradually increasing, which means that the average number of eclipses in a typical Saros series is decreasing.

Table 7 - Number of Anomalistic and Draconic Months in one Saros
Year	Anomalistic Months (223 Lunations)	Draconic Months (223 Lunations)	Node Shift (after 1 Saros)
-3000	238.991679	241.998742	0.4529
-2000	238.991763	241.998730	0.4571
-1000	238.991854	241.998717	0.4618
0	238.991950	241.998703	0.4668
yard	238.992051	241.998688	0.4722
2000	238.992157	241.998673	0.4779
3000	238.992267	241.998656	0.4838
4000	238.992379	241.998639	0.4899

Tabular array 8 shows how the number of draconic months is changing with respect to 358 synodic months (Inex menstruum) over a 7000-year interval. The mean shift in the lunar node after 1 Inex is much smaller than the Saros and is gradually decreasing. This explains why the lifetime of the Inex is then much longer than the Saros and is still increasing.

Table 8 - Number of Draconic Months in 1 Inex
Year	Draconic Months (358 Lunations)	Node Shift (afterward 1 Inex)
-3000	388.500223	-0.0801
-2000	388.500204	-0.0734
-1000	388.500183	-0.0659
0	388.500160	-0.0578
1000	388.500136	-0.0491
2000	388.500111	-0.0400
3000	388.500085	-0.0305
4000	388.500057	-0.0207

Although the Inex possesses a long lifespan, its mean duration is non easily characterized considering of the decreasing nodal shift seen in Table 8. If the instantaneous mean durations of the synodic and draconic months for the years -2000, +2000, and +4000 are used to calculate the mean duration of the Inex, the resulting lengths are near 14,500, 26,600, and 51,000 years, respectively (Meeus, 2004).

---

Acknowledgments

The information presented on this web page is based on material originally published in Five Millennium Canon of Solar Eclipses: -1999 to +3000 and Five Millennium Itemize of Solar Eclipses: -1999 to +3000.

Permission is freely granted to reproduce this data when accompanied past an acknowledgment:

"Eclipse Predictions by Fred Espenak (NASA's GSFC) and Jean Meeus"

---

References

Espenak, F., and Meeus, J., Five Millennium Canon of Solar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE), NASA Tech. Pub. 2006-214141, NASA Goddard Space Flight Center, Greenbelt, Maryland (2006).

Espenak, F., and Meeus, J., 5 Millennium Catalog of Solar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE), NASA Tech. Pub. 2008-214170, NASA Goddard Infinite Flight Middle, Greenbelt, Maryland (2008).

Gingerich, O., (Translator), Canon of Eclipses, Dover Publications, New York (1962) (from the original T.R. von Oppolzer, book, Catechism der Finsternisse, Wien, [1887]).

Meeus, J., Mathematical Astronomy Morsels III, Willmann-Bong, pp. 109-111, (2004).

Meeus, J., Grosjean, C.C., and Vanderleen, W., Catechism of Solar Eclipses, Pergamon Press, Oxford, U.k. (1966).

van den Bergh, G., Periodicity and Variation of Solar (and Lunar) Eclipses, Tjeenk Willink, and Haarlem, Netherlands (1955).

von Oppolzer, T.R., Canon der Finsternisse, Wien, (1887).

---

Return to:

Five Millennium Catalog of Solar Eclipses (web version)

Catalog of Solar Eclipse Saros Series

Eclipses and the Moon'southward Orbit

Periodicity of Lunar Eclipses

Eclipses and the Saros

---

bellabaces.blogspot.com

Source: https://eclipse.gsfc.nasa.gov/SEsaros/SEperiodicity.html

Share this post